Overview
Investigating the formation and evolution of dark matter halos, as the key building blocks of cosmic large-scale structure, is essential for constraining various cosmological models and further understanding our Universe. The highly non-linear dynamics involved nevertheless renders this a complex problem, with computationally costly simulations of gravitational structure formation currently the only tool to compute the non-linear evolution from initial conditions, yielding mock dark matter halo catalogues as the main output. However, running very large simulations of pure dark matter to generate fake observations of the full Universe several times is not feasible, requiring a large amount of memory and disk storage. A way to emulate such simulations, quickly and reliably, would be of use to a wide community as a new method for data analysis and light cone production for the next cosmological survey missions such as Euclid and Large Synoptic Survey Telescope. In this context, we employ a deep learning approach to construct an emulator to learn the mapping from dark matter density to halo fields.
Halo painting network
Our physical mapping network is inspired by a recently proposed variant of generative models, known as generative adversarial networks (GANs). In particular, we will use the key ideas in training WGANs, i.e. GANs optimized using the Wasserstein distance, to ensure that our network is able to paint halos well. A schematic of this Wasserstein mapping framework is provided in Fig. 1. Our generator is the halo painting network whose role is to learn the underlying non-linear relationship between the input 3D density field and the corresponding halo count distribution. Our critic provides as output the approximately learned Wasserstein distance between the real and predicted halo distributions. Intuitively, this Wasserstein distance can be interpreted as the amount of work required to transform a given probability distribution into the desired target distribution. This distance therefore corresponds the loss function that must be minimized to train the halo painting network.
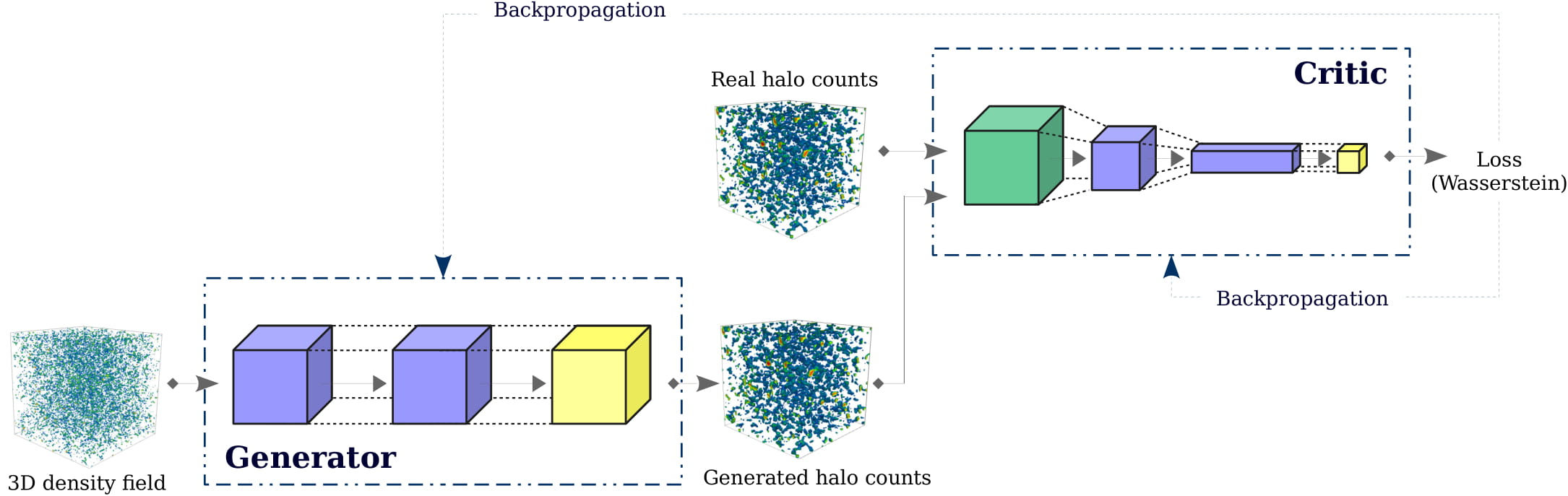 Schematic representation of Wasserstein halo painting network implemented in this work.
The role of the generator is to learn the underlying non-linear relationship between the
input 3D density field and the corresponding halo count distribution. The difference
between the output of the critic for the real and predicted halo distributions is the
approximately learnt Wasserstein distance and is used as the loss function which must be
minimized to train the generator.
Schematic representation of Wasserstein halo painting network implemented in this work.
The role of the generator is to learn the underlying non-linear relationship between the
input 3D density field and the corresponding halo count distribution. The difference
between the output of the critic for the real and predicted halo distributions is the
approximately learnt Wasserstein distance and is used as the loss function which must be
minimized to train the generator.
Remarkable performance of halo painting emulator
We showcased the performance our halo painting model using quantitative diagnostics. As a preliminary qualitative assessment, we performed a visual comparison. Fig. 2 depicts the reference and predicted halo distributions. Qualitative agreement is impressive, implying that the halo painting network is capable of mapping the complex structures of the cosmic web, such as halos, filaments and voids, to the corresponding distribution of halo counts.
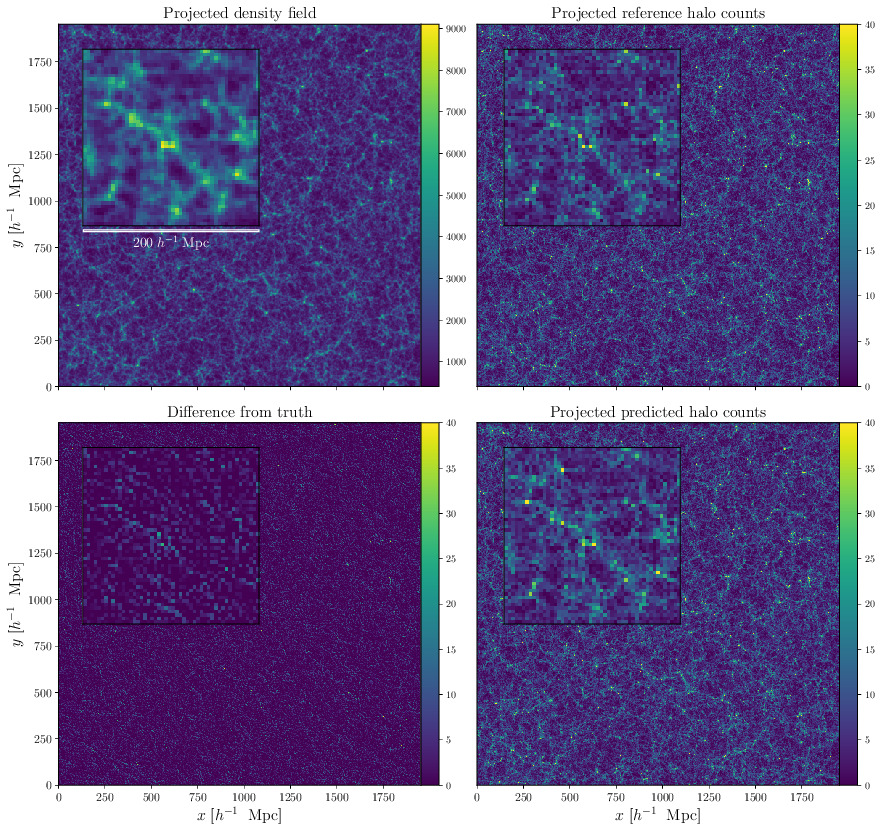 Prediction of 3D halo field by our halo painting model for a slice of depth \(\sim 100h^{-1}\) Mpc
and side length of \(\sim2000h^{-1}\) Mpc. A blind validation dataset is shown in the top right
panel, with the predicted halo count depicted below it. The corresponding second order Lagrangian Perturbation Theory (2LPT) density field is
displayed in the top left panel, with the difference between the reference and predicted halo
distributions depicted in the lower left panel. A visual comparison of the reference and predicted
halo count distributions indicates qualitatively the efficacy of our halo painting network.
Prediction of 3D halo field by our halo painting model for a slice of depth \(\sim 100h^{-1}\) Mpc
and side length of \(\sim2000h^{-1}\) Mpc. A blind validation dataset is shown in the top right
panel, with the predicted halo count depicted below it. The corresponding second order Lagrangian Perturbation Theory (2LPT) density field is
displayed in the top left panel, with the difference between the reference and predicted halo
distributions depicted in the lower left panel. A visual comparison of the reference and predicted
halo count distributions indicates qualitatively the efficacy of our halo painting network.
Power spectrum
As quantitative assessment, the standard practice in cosmology is to use summary statistics. These summary statistics provide a reliable metric to evaluate our halo painting network in terms of their capacity to encode essential information. Assuming the cosmological density field is approximately a Gaussian random field, as is the case on the large scales or at earlier times, the power spectrum provides a sufficient description of the field. We therefore demonstrated the capability of our network in reproducing the power spectrum of the reference halos. The left panel of Fig. 3 illustrates the extremely close agreement of the 3D power spectra of the reference and predicted halo fields.
We investigated the influence of the fiducial cosmology adopted for the simulations on the efficacy of our halo mapping model. In the right panel of Fig. 3, we show the network predictions for two cosmology variants in terms of their respective transfer functions, which is the ratio of the square root of the ratio of the predicted to reference power spectra. The corresponding transfer functions show a deviation of about \(10\%\) from the reference power spectra of their respective real halo distributions on the smallest and largest scales. This shows that our halo painting model is slightly sensitive to the underlying cosmology at the level of the power spectrum.
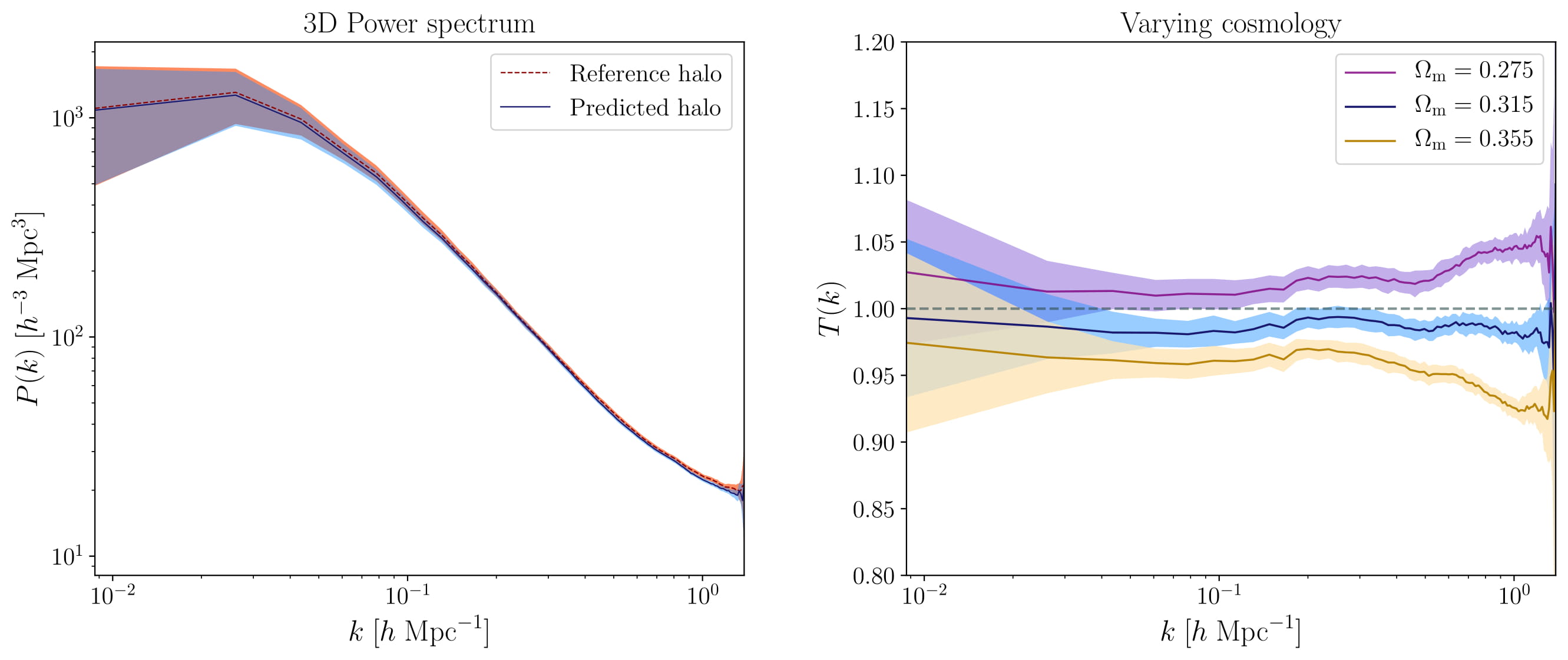 Left panel: Summary statistics of the 3D power spectra of the reference and predicted halo fields
for one thousand randomly selected patches. The solid lines indicate their respective means, while
the shaded regions indicate their respective \(1\sigma\) confidence regions, i.e. 68\% probability
volume. The above diagnostics demonstrate the ability of our halo painting model to reproduce the
characteristic statistics of the reference halo fields and therefore provide substantial
quantitative evidence for the performance of our neural network in mapping 3D density fields to
their corresponding halo distributions. Right panel: The corresponding transfer functions highlight
the consistency between the power spectra reconstructed from the predicted and real halo fields for
the three cosmology variants, with the deviation from their respective reference spectra being below
\(10\%\).
Left panel: Summary statistics of the 3D power spectra of the reference and predicted halo fields
for one thousand randomly selected patches. The solid lines indicate their respective means, while
the shaded regions indicate their respective \(1\sigma\) confidence regions, i.e. 68\% probability
volume. The above diagnostics demonstrate the ability of our halo painting model to reproduce the
characteristic statistics of the reference halo fields and therefore provide substantial
quantitative evidence for the performance of our neural network in mapping 3D density fields to
their corresponding halo distributions. Right panel: The corresponding transfer functions highlight
the consistency between the power spectra reconstructed from the predicted and real halo fields for
the three cosmology variants, with the deviation from their respective reference spectra being below
\(10\%\).
Bispectrum
The non-linear dynamics involved in gravitational evolution of cosmic structures contributes to a certain degree of non-Gaussianity of the cosmic density field on the small scales. Higher-order statistics are therefore required to characterize this non-Gaussian field. We used the bispectrum to quantify the spatial distribution of the density and halo fields. The bispectra reconstructed from the second order Lagrangian Perturbation Theory (2LPT), reference and predicted halo fields are displayed in Fig. 4. In particular, we show the bispectra for a given small- and large-scale configurations. The 2LPT halo field corresponds to a statistical description of the halo distribution, derived from the 2LPT density field, which is valid, by construction, at the level of two-point statistics and on large scales. This allows us to make a fair comparison between the clustering of the respective halo fields. The left panels of Fig. 4 demonstrate that our halo painting network reproduces the non-linear halo field both on the small and large scales, and is therefore capable of mapping the complex cosmic structures apparent in the reference halo field. Our network predictions also show a significant improvement over the corresponding 2LPT halo fields. In the right panels of Fig. 4, we find that there is a more significant dependence of our network on the fiducial cosmology at higher order statistics.
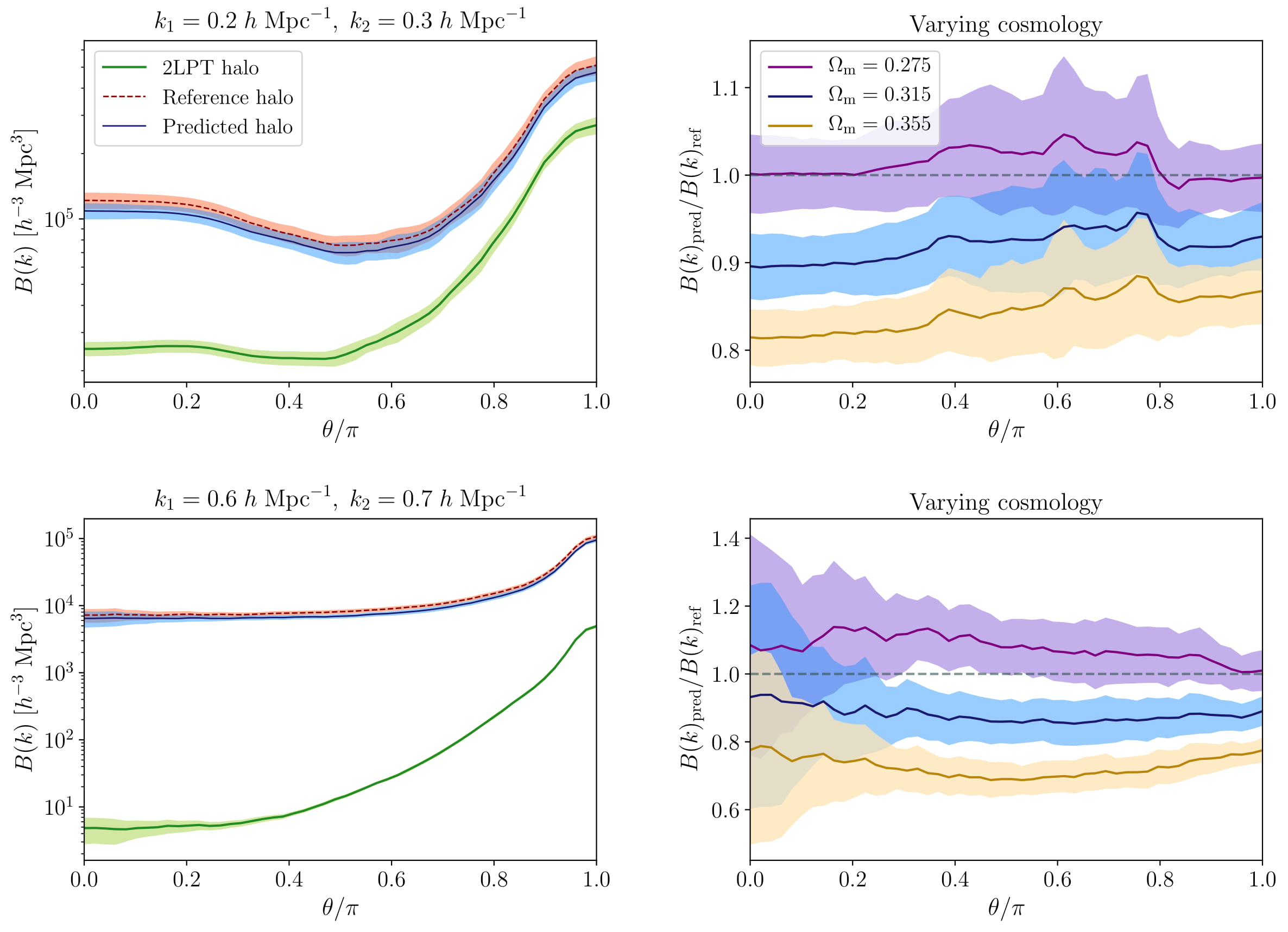 Left panels: Summary statistics of the 3D bispectra of the 2LPT, reference and predicted halo
fields for a given small- and large-scale configurations, as indicated by their respective titles.
In both cases, there is a close agreement between the bispectra from the reference and predicted
halo distributions. Our network predictions are a significant improvement over the corresponding
2LPT halo fields. Right panels: Deviation from the 3D bispectra of the reference halo distributions
of the corresponding predictions for the two cosmology variants. The above bispectrum diagnostics
show that our network is more sensitive to the fiducial cosmology than at the level of power spectrum.
The \(1\sigma\) confidence regions for five hundred randomly selected patches are depicted in each panel.
Left panels: Summary statistics of the 3D bispectra of the 2LPT, reference and predicted halo
fields for a given small- and large-scale configurations, as indicated by their respective titles.
In both cases, there is a close agreement between the bispectra from the reference and predicted
halo distributions. Our network predictions are a significant improvement over the corresponding
2LPT halo fields. Right panels: Deviation from the 3D bispectra of the reference halo distributions
of the corresponding predictions for the two cosmology variants. The above bispectrum diagnostics
show that our network is more sensitive to the fiducial cosmology than at the level of power spectrum.
The \(1\sigma\) confidence regions for five hundred randomly selected patches are depicted in each panel.
Key advantages
- Extremely efficient once trained. Our emulator is capable of rapidly predicting simulations of halo distribution based on a computationally cheap cosmic density field. For instance, the network prediction for a \(256^3\) simulation size requires roughly one second on the NVIDIA Quadro P6000.
- Can predict the 3D halo distribution for any arbitrary simulation box size. A large simulation box, therefore, does not require tiling of smaller sub-elements. More importantly, this implies that our neural network can be trained on smaller simulations and subsequently used to predict large halo distributions.
- Encodes mass information of halos, such that our method can predict the mass distribution of halos.
- Allows us to bypass ad hoc galaxy bias models and work in terms of better understood models.
Potential applications
- Fast generation of mock halo catalogues and light cone production. This would be useful for the data analysis of upcoming large galaxy surveys of unprecedented sizes.
- To fill in small-scale structure at a high resolution from low resolution large-scale simulations.
- As a component in Bayesian forward modelling techniques for large-scale structure inference (cf. BORG) or cosmological parameter inference (cf. ALTAIR) to accelerate the scientific process, rendering detailed and high-resolution analyses feasible. This would provide statistically interpretable results, while maintaining the scientific rigour.
References
- D. Kodi Ramanah, T. Charnock & G. Lavaux, 2019, submitted to PRD, arxiv 1903.10524

- A notebook tutorial to paint the halos of the article: notebook
- Source code repository: https://github.com/doogesh/halo_painting
Authored by D. K. Ramanah
Post identifier: /method/halo-painting