Overview

To probe the Universe on the cosmological scales, we employ large galaxy redshift catalogues which encode the spatial distribution of galaxies. However, these galaxy surveys are contaminated by various effects, such as the contamination from dust, stars and the atmosphere, commonly referred to as foregrounds. Conventional methods for the treatment of such contaminations rely on a sufficiently precise estimate of the map of expected foreground contaminants to account for them in the statistical analysis. Such approaches exploit the fact that the sources and mechanisms involved in the generation of these contaminants are well-known.

But how can we ensure robust cosmological inference from galaxy surveys if we are facing as yet unknown foreground contaminations? In particular, the next-generation of surveys (e.g. Euclid, LSST) will not be limited by noise but by such systematic effects. We propose a novel likelihood¹ which accurately accounts for and corrects effects of unknown foreground contaminations. Robust likelihood approaches, as presented below, have a potentially crucial role in optimizing the scientific returns of state-of-the-art surveys.

Robust likelihood

The underlying conceptual framework of our novel likelihood relies on the marginalization of the unknown large-scale foreground contamination amplitudes. To this end, we need to label voxels having the same foreground modulation and this is encoded via a colour indexing scheme that groups the voxels into a collection of angular patches. This requires the construction of a sky map which is divided into regions of a given angular scale, with each region denoted by a specific colour, as illustrated in Fig. 1 (a). The corresponding representation on a 3D grid results in a 3D distribution of patches, with the a given slice of the coloured grid depicted in Fig. 1 (b). The collection of voxels belonging to a particular patch is employed in the computation of the robust likelihood.

Our proposed data model is conceptually straightforward and provides a maximally ignorant approach to deal with unknown systematics, with the colouring scheme being independent of any prior foreground information. As such, the numerical implementation of our novel likelihood is generic and does not require any adjustments to the other components in the forward modelling framework of BORG (Bayesian Origin Reconstruction from Galaxies) for the inference of non-linear cosmic structures.

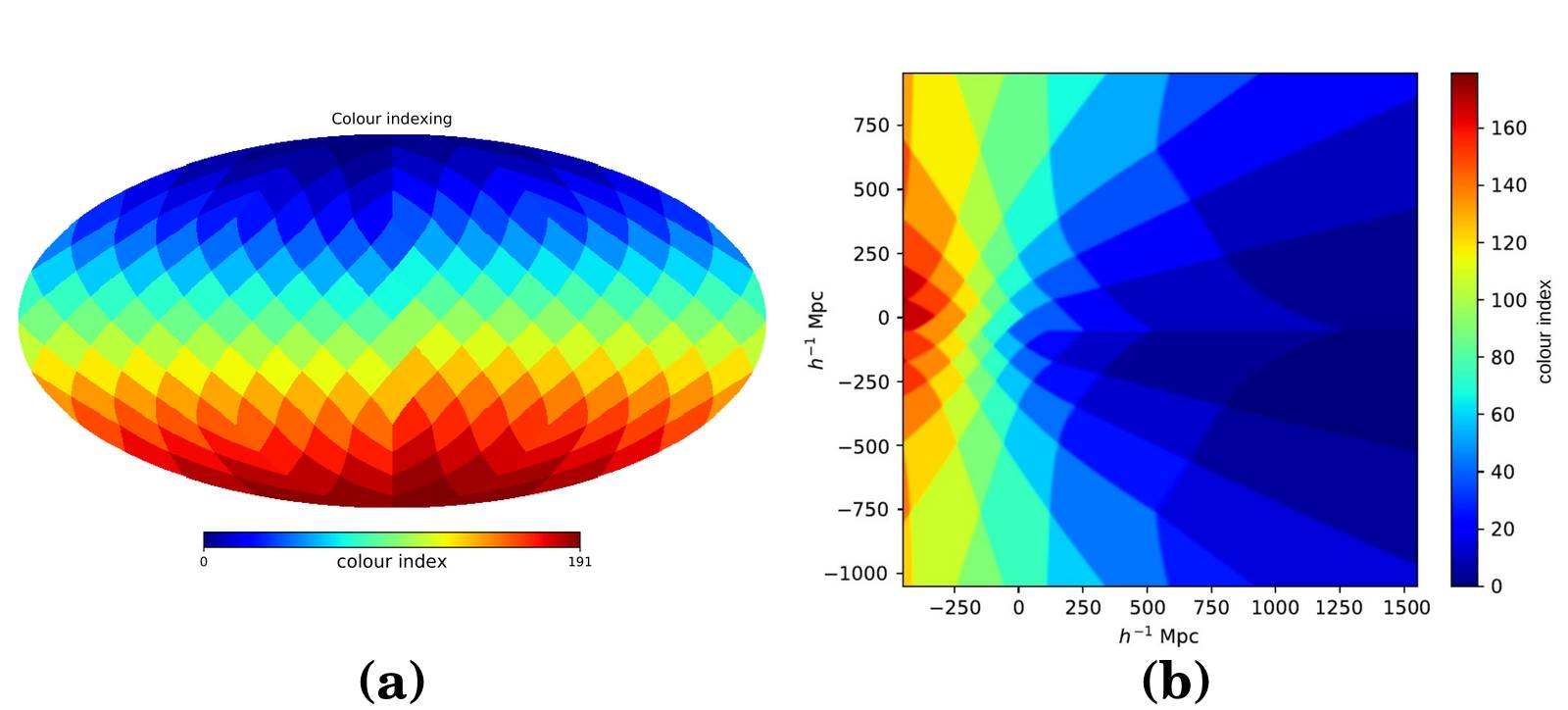(a) Schematic to illustrate the colour indexing of the survey elements. Colours are assigned to patches of a given angular scale. (b) Slice through the 3D coloured box resulting from the extrusion of the colour indexing scheme on the left panel onto a 3D grid. This collection of coloured patches is subsequently employed in the computation of the robust likelihood.

Comparison with a standard Poissonian likelihood analysis

We showcase the application of our robust likelihood to a mock data set with significant foreground contaminations and evaluated its performance via a comparison with an analysis employing a standard Poissonian likelihood, as typically used in modern large-scale structure analyses. The results illustrated below clearly demonstrate the efficacy of our proposed likelihood in robustly dealing with unknown foreground contaminations for the inference of non-linearly evolved dark matter density fields and the underlying cosmological power spectra from deep galaxy redshift surveys.

Inferred dark matter density fields

We first study the impact of the large-scale contamination on the inferred non-linearly evolved density field. We compare the ensemble mean density fields and corresponding standard deviations for the two Markov chains obtained using BORG with the Poissonian and novel likelihoods, respectively, illustrated in the top and bottom panels of Fig. 2, for a particular slice of the 3D density field. As can be deduced from the top left panel of Fig. 2, the standard Poissonian analysis results in spurious effects in the density field, particularly close to the boundaries of the survey since these are the regions that are the most affected by the dust contamination. In contrast, our novel likelihood analysis yields a homogeneous density distribution through the entire observed domain, with the filamentary nature of the present-day density field clearly seen. From this visual comparison, it is evident that our novel likelihood is more robust against unknown large-scale contaminations.

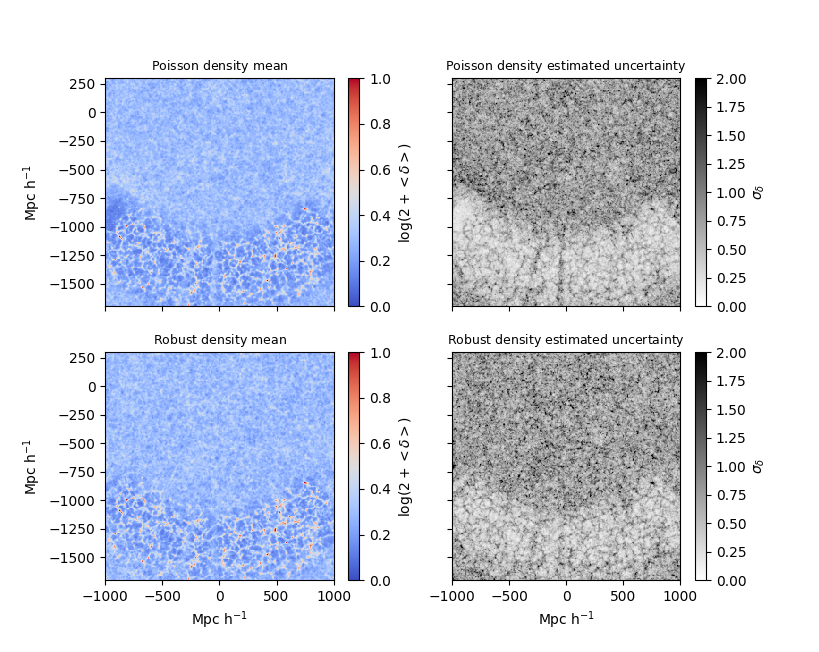Mean and estimated uncertainty of the non-linearly evolved density fields, computed from the sampled realizations of the respective Markov chains obtained from both the Poissonian (upper panels) and novel likelihood (lower panels) analyses, with the same slice through the 3D fields being depicted. Unlike our robust data model, the standard Poissonian analysis yields some artefacts in the reconstructed density field, particularly near the survey boundary, where the foreground contamination is stronger.

Reconstructed matter power spectra

From the realizations of our inferred 3D initial density field, we can reconstruct the corresponding matter power spectra and compare them to the prior cosmological power spectrum adopted for the mock generation. The top panels of Fig. 3 illustrates the inferred power spectra for both likelihood analyses, with the bottom panels displaying the ratio of the a posteriori power spectra to the prior power spectrum. While the standard Poissonian analysis yields excessive power on the large scales due to the artefacts in the inferred density field, the analysis with our novel likelihood allows us to recover an unbiased power spectrum across the full range of Fourier modes.

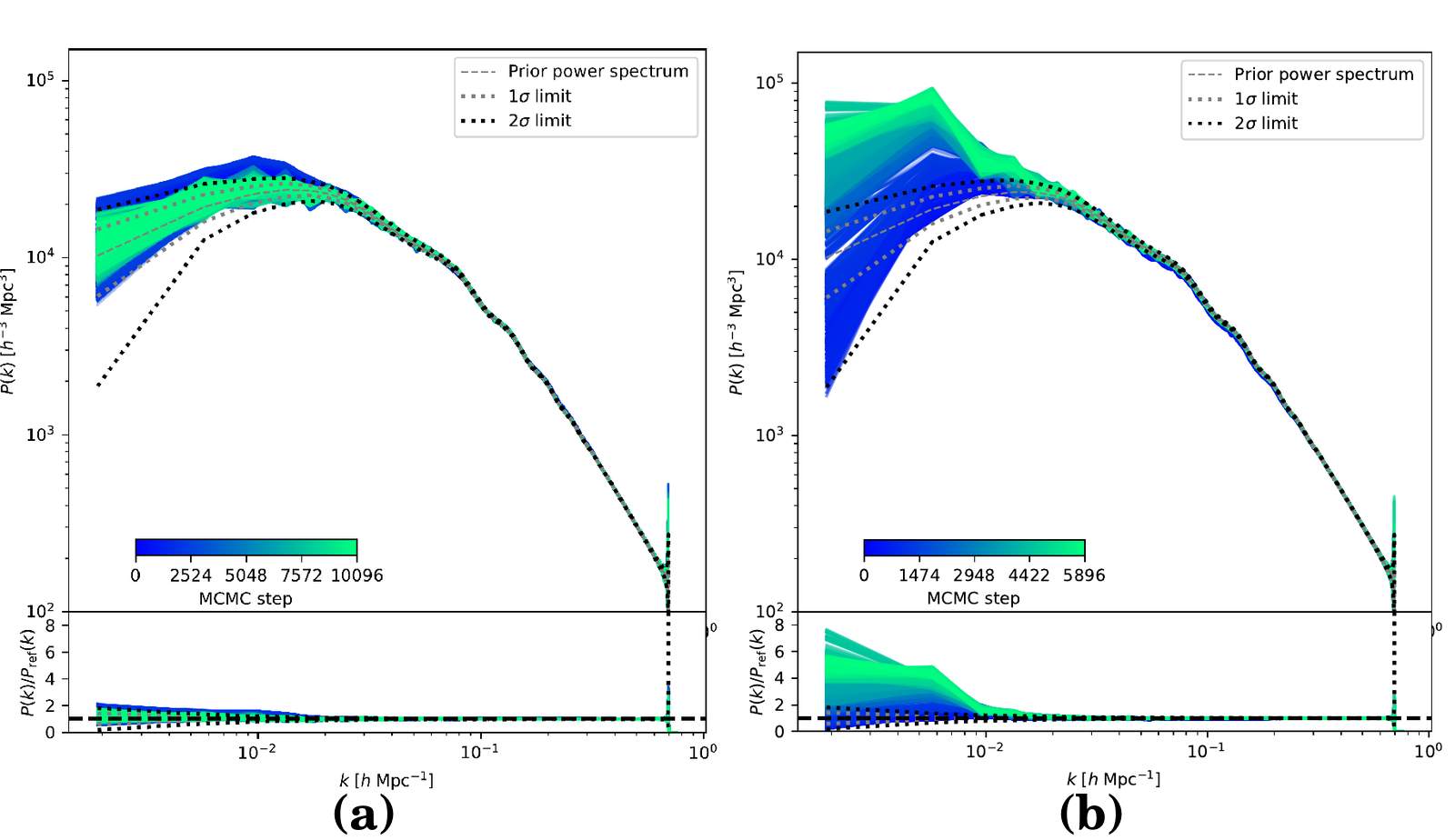Reconstructed power spectra from the inferred initial conditions from the BORG analysis for the robust likelihood (left panel) and the Poissonian likelihood (right panel). The power spectra of the individual realizations, after the initial burn-in phase, from the robust likelihood analysis possess the correct power across all scales considered, demonstrating that the foregrounds have been properly accounted for. In contrast, the standard Poissonian analysis exhibits spurious power artefacts due to the unknown foreground contaminations, yielding excessive power on these scales.